Salut Damien,
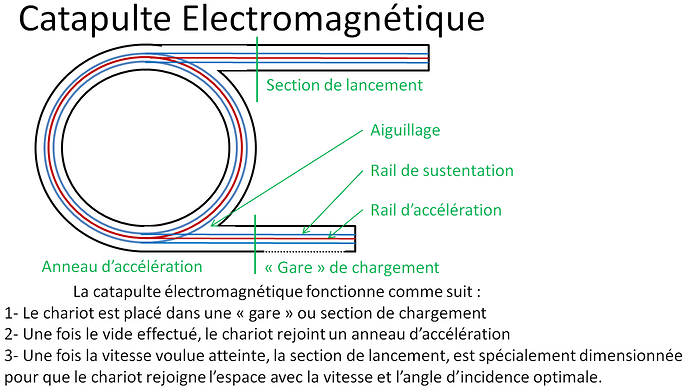
Le choix de la boucle dans le cas de Spinlaunch est surprenant.
Lorsqu’on s’intéresse au sujet, on arrive assez rapidement à la conclusion qu’une difficulté majeur de ce projet vient de la force centrifuge et que la configuration la plus performante consiste en un arc de cercle orienté vers le haut.
Si je reprends les paramètres du projet StarTram Generation 1 du premier message, soit 30g et 8780m/s, j’arrive aux paramètres suivants:
Soit la force centrifuge a=v^2/r
Pour a = 300m/s^2 (30g), on a:
a*r=v^2
r=v^2/a
r=8780^2/300
r=256961m
Soit un rayon d’environ 257km, ou encore 1614km de circonférence.
Avec un tunnel linéaire pour une même accélération on a:
d=a/2 * t^2 et v=a*t
Soit t = 8780/300 = 29.266s
et d = 300/2 * 29.266^2 = 128480m
Soit une longueur de tunnel de 128km vs 1614km
La configuration linéaire présente une économie d’un facteur 12!
Reste le problème de l’angle d’élévation. Il faut courber le tunnel vers le haut, mais avec un rayon suffisamment élevé, toujours à cause de la force centrifuge, donc creuser profond.
La longueur du tunnel est inversement proportionnelle à l’accélération supportée par le satellite. On a donc intérêt à augmenter les g. Si on passe à 100g ce qui reste supportable mécaniquement, on réduit la longueur à 38km.
Les trois autres points difficiles sont: la décélération dans l’atmosphère, l’échauffement du projectile et l’interface entre le tube sous vide et la sortie.
Les deux premières difficultés sont inversement proportionnelles à l’échelle du projectile et à l’angle d’élévation, la durée de passage dans l’air étant inversement proportionnel à celui-ci.
L’échauffement est un problème majeur. Wikipédia donne 30kw/cm^2 à dissiper ce qui est déjà énorme, alors que le coefficient de traînée (Cx) indiqué est de 0,09, ce qui me semble très optimiste en supersonique. Il me semble sauf erreur que le Cx du Concorde passe autour de 1 lors du passage en mode supersonique, l’écoulement de l’air passant du mode laminaire à turbulent. Quelqu’un du CNES pourrait peut-être confirmer? 
, j’ai plein de concepts à pour réaliser une catapulte électromagnétique pour CubeSats.
